What Is Simple Harmonic Motion?
Many simple
oscillators display the characteristic of Simple Harmonic Motion (SHM).
Examples are springs, pendula, waves on the sea... all of which move
in a predictable way and follow a certain pattern. Oscillators demonstrating
SHM have displacement-time graphs that can be related to the graph of
![]() or
or ![]() plotted
against
plotted
against ![]() , in other words
regular Sine or Cosine curves.
, in other words
regular Sine or Cosine curves.
Oscillators in simple harmonic motion follow several equations. These are related to different factors about the oscillator. For the purposes of this document I will confine these equations to springs, which can easily be used to test the ideas put forward.
An alternative derivation of SHM is also available, which uses a theoretical experiment to obtain by logical progression the proportionality contained in the equation.
From Hooke's Law we know that Force exerted by a spring on a mass attached to it is directly proportional to the extension of the spring, or:
![]()
Where F is the force exerted on the spring and x is the extension of the spring from its normal length. From this we can see that the equation relating these two vectors is:
![]()
Where k is Hooke's constant.
From this equation, and therefore from the slope of a Force against Displacement graph, we can calculate k.
With a mass with
weight W Newtons attached but at rest, the spring stretches by
distance ![]() . This then
means that:
. This then
means that:
![]()
as the force provided by the spring must be equal to the downward force provided by the mass.
If we pull the weight down a further distance x, the restoring force, F provided by the spring in an upwards direction acting on the mass is F+W. As at this position:
![]()
Applying Newton's second Law of Motion, F=ma gives us:
![]()
As we know that from Hooke's Law for W the spring extends a certain distance:
![]()
We can then say:
![]()
Which can then be cancelled to give:
![]() or
or
![]()
This then relates a spring's Hooke's constant to the acceleration acting on a certain mass.
From one of the equations for SHM we can derive another equation:
![]()
comparing this with the above equation derived from F=ma:
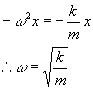
As the period, T, of the motion of the mass on the spring is given by the general equation:
![]()
we can substitute to give:
![]()
where m is, in this case, the mass on the spring and k is the stiffness of the spring.
![[Opinions: Statue at the University of Twente, Enschede, The Netherlands]](images/opinions.jpg)