Derivation of the Simple Harmonic Motion Equation
This page
shows how the equation (or rather proportionality) for the equation
for the S.H.M. of a spring/trolley oscillator system can be derived.
Its level is not meant to be above that expected at higher level GCSE/first
year of A-Level.
The preliminary
data are as follows:
Consider a trolley
connected between two sets of springs of different spring constants.
In both arrangements the trolley has the same mass and the same amplitude
of oscillation is used. The period in (a) is twice that of (b) and therefore
(b) oscillates at twice the speed of (a).
From this
information we can see the following:
At the point of
rest, or the origin (the middle of the oscillation), when the trolleys
are oscillating they have their highest velocity at this point.
If we take the
maximum displacement of the trolleys to be x, we can therefore
say that in one complete oscillation both trolleys move 4x.
From the displacement-time
graphs (which were provided: they are sinusoidal) we can see that the
period of the trolleys is the following:
Trolley (a) T
Trolley (b) T/2
(taking the period
of (a) as being T, the period of (b) must be half).
Therefore the average
speeds of the trolleys are:
Trolley (a) 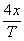
Trolley (b) 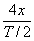
From this we can
say that Trolley (b) has twice the speed of (a).
As the trolleys
reach maximum speed when they travel to the midpoint of their oscillations,
we can say that the time taken to reach this maximum speed is equal
to one quarter of their respective periods (as in one complete oscillation
the pass through the origin twice). Therefore the time taken for the
trolleys to reach maximum velocity is:
Trolley (a) T/4
Trolley (b) 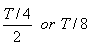
If we take the maximum
velocity of the trolley (a) as being v, we can say that the maximum
speed of trolley (b) is twice that of (a), as it covers the same distance
in half the time. This is therefore 2v. From this we can calculate
the average acceleration of the trolleys:
Trolley (a) 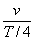
Trolley (b) 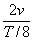
Which can be simplified
to give:
Trolley (a) 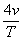
Trolley (b) 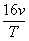
Therefore (b) has
4 times the average acceleration of (a).
From Newton's second
Law, we know that F=ma, therefore
as m is constant F is directly proportional to a.
This then means that if a is increased four times, F is also increased
by the same factor. We can therefore say that:
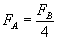
(Where these are
the forces acting on the respective trolleys).
From Hooke's Law,
we can see that as x, (the amplitude of oscillation) is constant,
F is directly proportional to k, therefore if F
is increased by a factor of 4, (as in the example above), k must
have increased by the same factor. From this we can see that the spring
in (b) must have four times the Hooke's constant of the spring in (a).
Looking at what
has been derived above, we can therefore see that the period of oscillation
follows an inverse square law in relation to the Hooke's constant of
the spring. This is because we can see that the period decreases as
the Hooke's constant of the spring increases. Using the data provided,
it can be seen that as k quadruples the period halves. This therefore
suggests that:
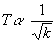 Looking at it in
the light of acceleration, we can see that when this quadruples the
period halves. Therefore, the relationship between period and acceleration
is follows an inverse square law:
Looking at it in
the light of acceleration, we can see that when this quadruples the
period halves. Therefore, the relationship between period and acceleration
is follows an inverse square law:
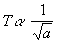
Using Newton's
second Law, we can see that, if the mass stays constant the following
is true:
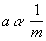
Therefore, if we
substitute this into the proportionality connecting period with acceleration
we find that:
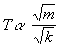 This relationship
therefore connects period to mass and the Hooke's constant of the spring.
To make it an equation, we must put in a constant. This constant is
This relationship
therefore connects period to mass and the Hooke's constant of the spring.
To make it an equation, we must put in a constant. This constant is
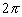 . Hence:
. Hence:
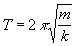
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Opinions: Statue at the University of Twente, Enschede, The Netherlands]](images/opinions.jpg)